Do we live in a world with bubbles?

The interest in financial bubbles is supported by several empirical works revealing that asset prices fluctuate more than the underlying fundamentals. In particular, Shiller (1981), in a study of a composite asset price series, Standard and Poor’s, from 1871 to 1979 and of the Dow Jones industrial index from 1928 to 1979, measures stock volatility as five times that of real dividends. More recent work (Martin and Ventura (2012)) confirms that asset price volatility cannot be explained by fundamental volatility. These various contributions therefore highlight the existence of speculative bubbles.

Moreover, financial crises are often closely linked to the bursting of speculative bubbles, and frequently follow episodes of concomitant growth of a speculative bubble and GDP. The 2007 crisis, which originated in the subprime crisis, is a striking example. History teaches us that bubble episodes, and the financial crises that often follow their bursting, appear periodically. Famous examples include the seventeenth-century tulipomania in Holland, the 1720 financial crash in London that followed speculation between 1711 and 1720, and the financial crisis in the U.K. that led to the collapse of the U.K. stock market.

The idea that bubbles can reflect irrational behavior is an old one. Regarding the South Sea Company bubble that caused the 1720 stock market crisis in Great Britain, Newton is reported to have said: "I can calculate the motions of erratic stars, but not the madness of the multitude". This traditional view is still present in debates on the evolution of financial assets. In 1996, Alan Greenspan spoke of «irrational exuberance» to describe the movement of bubbles in financial markets.

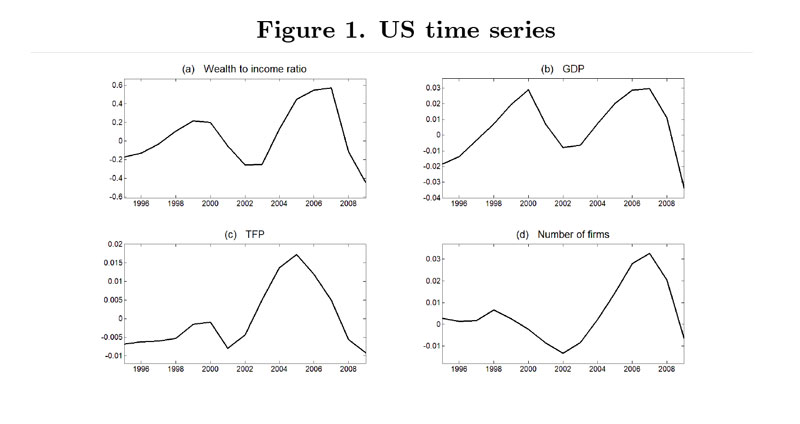
Figure. US time series Source.
Clain-Chamosset-Yvrard, L. and Raurich, X. and Seegmuller, T., 2023, "Entrepreneurship, Growth and Productivity with Bubbles", Working Paper.

However, there is no consensus among economists on the idea that speculative bubbles can only be explained by the irrational behavior of traders, even though they have sought to determine whether forms of bounded rationality can better explain the evolution of asset prices. The question that has arisen is whether the existence of bubbles can be explained by the rational behavior of agents. This is the approach we will follow here. We will discuss results on the existence and features of bubbles that emerge from the macrodynamic literature with rational agents.

We recall that a bubble is defined as the difference between the market price of an asset and its fundamental value, i.e. the sum of expected future dividends. Of course, expectations play a crucial role in bubbles: a high price today is justified by optimistic expectations about the future price. The existence of a bubble on an asset requires this asset to be resaleable, and therefore new traders must be able to participate in the market every period. Through its demographic aspects, the overlapping generations model provides such a structure, because not all traders participate in the trading market at the same time.

The first question is the existence of equilibria with bubbles. A stationary equilibrium with a bubble coexists with one without a bubble if the interest factor of the equilibrium without a bubble is sufficiently low. The stationary bubble then obeys the golden rule, i.e. an efficient solution. In contrast, the equilibrium without a bubble is inefficient because it is characterized by too low savings. The existence and the formation of the bubble make up for savings unachieved.

These results that can be obtained from an exchange economy are not drastically different when there is production, except that they can be linked to the level of capital. The existence of a stationary state with a bubble still requires a stationary state without a bubble characterized by a sufficiently low gross return on capital (Tirole (1985)). This means that the latter over-accumulates capital and is dynamically inefficient. The bubbly stationary state, which again complies with the golden rule, is thus associated with a lower level of capital. The existence of the bubble, which stems from a desire to over-save, leads to a crowding-out effect on capital. This important result of the existence of a bubble in the presence of capital has been criticized for two reasons: dynamic inefficiency lacks empirical validity (Abel et al. (1989)), and bubble episodes are instead characterized by phases of increased production (Martin and Ventura (2012), among others).

As mentioned earlier, the question of expectations is crucial to understand the existence and sustainability of bubbles. The analysis of a market crash is of course related, and was first addressed by Weil (1987). He introduced a positive probability of bubbles bursting which expresses the volatility of agents’ expectations. When a bubble exists, agents can coordinate their expectations either on the equilibrium with a bubble, or on the equilibrium without a bubble. In this economy, there is a stationary sunspot equilibrium with a stochastic bubble, if the probability of the bubble bursting is not too high. This result is important, because this is still the way bubble crashes are introduced in most of the current analysis.

Bubbles are not impossible when agents have infinite lifetimes and horizons, if the behavior of agents mimics overlapping generations. As shown by Kocherlakota (1992), an equilibrium with a positive bubble can exist when heterogeneous agents are alternatively constrained by the impossibility of short-selling. Since traders are prevented from borrowing against their entire future income, assets can be positively valued. Financial imperfections are therefore crucial to understanding bubbles.

These market imperfections also play an important role in explaining some features of bubbles and responding to some weaknesses of earlier analysis. One key question is that of understanding the positive correlation between episodes of bubbles and growth. Following Farhi and Tirole (2012) or Martin and Ventura (2012), imagine that agents are heterogeneous and face financial constraints. Agents do not have the same opportunities to invest. The most productive will invest in capital. To do so, they will borrow against a financial constraint that generates an investment multiplier. They will also sell liquid financial assets, including the bubble, to less productive agents, to increase their capital investment. This gives the bubble its liquidity role, which explains why phases of bubble growth are accompanied by an increase in productive capital, and a bubble crash by a sharp drop in production, as we observe in data.

Recent research aims to explain additional features of bubbly episodes. Among others, what is the link with entrepreneurship? A growing bubble can be consistent with an increasing number of entrepreneurs, even though such a trend is associated with an interest rate rise promoting savings. Because wealth increases too, entrepreneurs are better able to pay entry costs. Another question concerns the relationship with total productivity. The positive correlation with bubbly episodes can be explained when the most productive firms are also the largest ones and benefit more from the increased wealth associated with bubbly episodes. Some researchers have also explored why larger bubbles are linked to an increase in labor, while bubble crashes engender higher unemployment. The main reason is that employment is positively correlated to production, and therefore often operates via one of the above mechanisms.

Another important concern of the macroeconomic view of bubbles is, of course, the role of public policies. An important debate focuses on the stabilizing role of monetary policies when there are bubbles in the economy. There are no general conclusions, but raising the interest rate cannot always be considered to have a stabilizing effect, because this also increases bubbles, which immediately react to the interest rate rise. Some contributions argue that a relevant monetary policy should react to the price of financial assets. Another way of thinking about policies is to determine whether a public policy can rule out the negative impact of a bubble crash. The introduction of public debt can play this role since it evolves in the same way as bubbles and can have the same impacts on liquidity and savings. Therefore, it can be an appropriate substitute for a bubble under a market crash. Finally, it is important to note that the emergence of a bubble strongly depends on the distribution of income throughout the life-cycle, because this distribution creates the incentive to save and borrow at different ages. As a direct implication, the taxation of labor and capital incomes can be a significant determinant of the existence and features of bubbles, modifying the distribution of income throughout the life-cycle. If we consider that we live in a world with bubbles, all these subjects invite further investigation.