Mathieu Faure & Nicolas Gravel, 2021, International Economic Review, vol. 62(1), 357-404
THE BROADER RESEARCH PROGRAM
A fundamental achievement of the modern theory of inequality measurement is the early demonstration by the mathematicians Hardy, Littlewood and Polya that four seemingly different definitions of «undisputable equalization» are actually equivalent. The first definition is the well-known principle of Pigou-Dalton transfers. The second definition is more ethical in nature and requires consensus among all inequality averse welfarist ethical observers who assume that agents transform income into well-being by the same increasing and concave function. The third and fourth definitions provide empirically implementable tests. One of the two tests is Lorenz dominance, while the other is poverty reduction for all poverty lines, with poverty measured by the minimum income required to eliminate poverty with respect to the line.
While this equivalence is foundational to inequality measurement, it only concerns distributions of one cardinally measurable attribute – such as income - between otherwise homogeneous agents. Yet income is not the only relevant source of differentiation between economic agents. If these agents are communities such as households or jurisdictions, they differ not only in their total income but also in number of members. If the agents are individuals, they may also differ in characteristics such as age, health, education or effort. What does «undisputably reducing inequalities» in income mean when applied to agents who differ with respect to another characteristic? This is the basic question addressed in this paper.
PAPER’S CONTRIBUTIONS
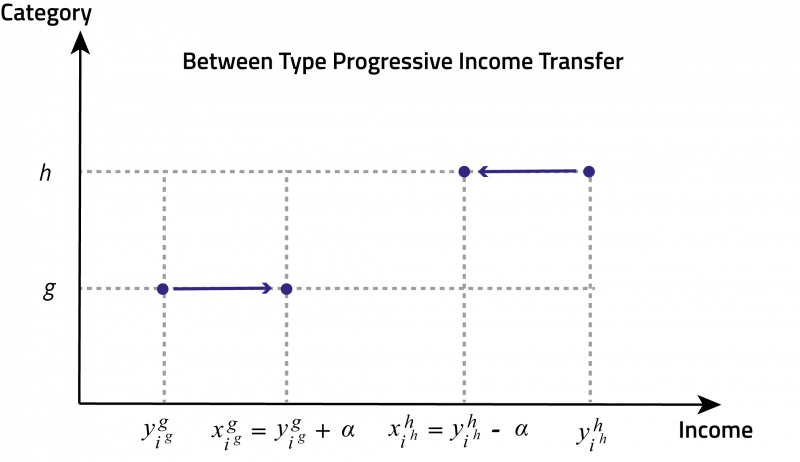
This paper establishes an equivalence between four definitions of «undisputable equalization» of income among agents vertically differentiated with respect to a non-income characteristic, each of these definitions being analogous in nature to the definitions for homogenous agents. The first definition is the possibility of going from one distribution to the other by a finite sequence of income transfers from richer and more highly ranked agents to poorer and less highly ranked ones. This can be seen as a weakening of the principle of Pigou-Dalton transfer, limiting its scope to agents who can be ordered both by their income and by the other characteristic. The second definition is that underlying a consensus among inequality-averse welfarist ethical observers who assume that all agents transform income into wellbeing by the same utility function, which is increasing and concave with respect to income only and whose marginal utility of income is decreasing with respect to the other characteristic. The third definition is similar to poverty reduction for all poverty lines, but with the poverty lines allowed to be a nonincreasing function of the other characteristic. The intuition is that being poor in income is more difficult for a healthy person than for an otherwise identical person who is ill. The fourth definition is similar in spirit to Lorenz dominance and views as «undisputably equalizing» any transformation in the income distributions that increases the total income of the k poorest agents, no matter what k is. However, it is not straightforward to define who these k-poorest agents are when the agents differ in another characteristic. Our paper provides such a definition and shows that it gives rise to a Lorenzlike criterion whose dominance is equivalent to the three other notions of equalization.
Prior to this paper, attempts were made to examine the connections between some of the above definitions. However, no proof of the equivalence between the transfer-based notion of equalization and either the welfarist or the poverty criterion was ever obtained. An important contribution of this
paper is to provide such a proof, one that has turned out to be rather challenging. The proof actually involved constructing an algorithm for going from a distribution y to a distribution x by a finite sequence of inequality-reducing transfers that is based solely on the information that x dominates y as per the ordered poverty gap criterion. Another important accomplishment of the paper is the discovery of a generalization of Lorenz dominance that can be used to compare distributions of incomes among vertically differentiated agents.
FUTURE DIRECTIONS
There are at least three directions in which the analysis of this paper could be extended. One of them concerns applications of the implementable dominance criteria characterized in our paper. Poverty dominance for all increasing poverty lines is a somewhat simple criterion that has not been used much in empirical analysis, even though some authors have shown that it is easily amenable to statistical inference techniques. It is our hope that the arguments we provide in its favour will encourage its use in empirical work. Another direction for future research would be to better appraise the performance of the two implementable criteria - poverty dominance and our new Lorenz-like dominance criterion - in terms of computational complexity. A third potential direction for future research would be to identify inequality indices compatible with the incomplete ranking of distributions that we have characterized.
→ This article was issued in AMSE Newletter, Summer 2021.