Luc Bauwens, Guillaume Chevillon, and Sébastien Laurent, 2023, Journal of Econometrics, Volume 236, Issue 1.
»
We provide a novel multivariate methodology for modeling and forecasting series displaying long memory,
but using just one lag instead of an infinite history.
RESEARCH PROGRAM
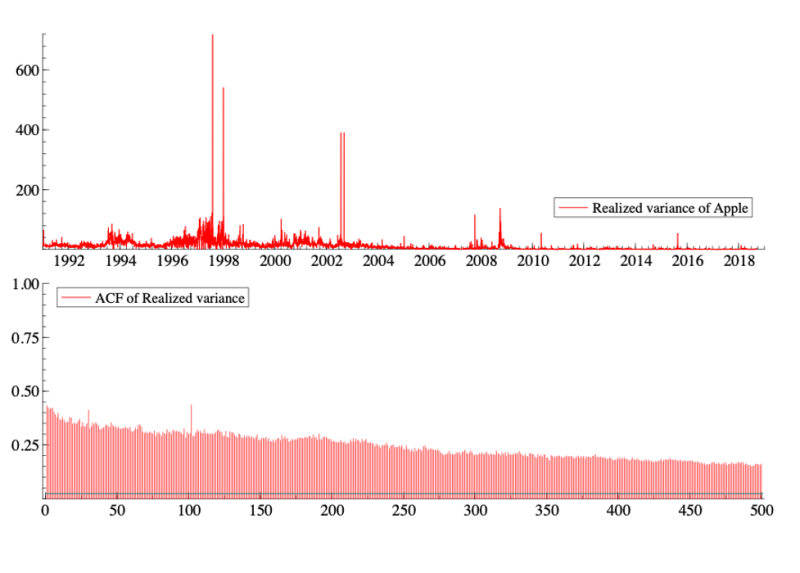
Many series, like the daily realized variance of Apple stock (computed as the sum over one day of 5-minute squared log-returns in %) plotted in the top panel of the figure below, display long memory. Long memory is characterized by a very slowly decreasing autocorrelation function (ACF), as illustrated in the bottom panel of the figure, whereas in short-memory processes, the ACF decays exponentially. This figure suggests that today’s realized variance (i.e., a risk measure) has a correlation of about 15% with the realized variance 500 days ago (approximately 2 years).
Many economic, financial, and also hydrological series share this property. Looking at the above graph, the natural choice seems to be a timeseries model that uses the very distant past to predict the future values of the series (such as an ARFIMA model). But is it rational to use such distant observations to predict tomorrow’s risk when we know that financial markets react very quickly to new information? Could this long memory be hiding something else?
The econometric literature has found that long memory can have different origins, such as aggregation of short-memory processes, linear modeling of a nonlinear process, structural changes or agents’ self-referential learning behaviors and forward expectations.
In 2018, two papers published in Econometrica and Journal of Econometrics, respectively by Schennach and Chevillon, Hecq, and Laurent, proved that long memory can arise in individual series linked within an infinite dimensional network or system. More specifically, they show that long memory can result from the marginalization of a large dimensional system. They provide a parametric framework under which the variables of an n-dimensional vector autoregressive model of order 1, i.e., a VAR(1), display long memory when modeled using a univariate model like an ARFIMA (i.e., modeling the n-series independently rather than the full system).
PAPER’S CONTRIBUTION
A model with just one lag can therefore generate long memory. But how can we use this finding empirically? In the article “We modeled long memory with just one lag!”, forthcoming in Journal of Econometrics, Bauwens, Chevillon, and Laurent (2023) provide a novel multivariate methodology for modeling and forecasting series displaying long memory, but using just one lag instead of an infinite history. They model long-memory properties within a vector autoregressive system of order 1 and consider Bayesian estimation or ridge regression. To do so, they derive a theorydriven parametric setting that informs a prior distribution or a shrinkage target. Their proposal significantly outperforms univariate timeseries long-memory models when forecasting a daily volatility measure for 250 U.S. company stocks over twelve years. This provides empirical validation of theoretical results showing that long memory can be the cause of the marginalization of a large-scale system.
FURTHER RESEARCH
This article shows how to predict the long memory of an observed risk measure, namely the realized variance calculated from 5-minute financial returns, using a high-dimensional VAR(1) model. The approach involves two steps. First, the risk measure is calculated using a non-parametric approach (i.e., the realized variance). Then a model is estimated to predict the conditional mean of this series, using either a Bayesian estimation or a ridge regression.
However, intraday data is not always available, which makes it impossible to calculate a realized measure of the variance. This is why researchers and practitioners often rely on parametric models such as (G)ARCH models or FIGARCH models (in the presence of long memory) to forecast volatility. In this case, the latent conditional variance is induced by a parametric model estimated on daily returns and not fitted to an observed measure of risk. The next step in this series of projects is to adapt the estimation of ARCH-type models to the theoretical framework mentioned above, using either Bayesian or penalized likelihood methods.
It would also be worth checking whether the above framework can be used to model and predict other long-memory series that can be assumed to belong to a large system.
→ This article was issued in AMSE Newletter, Summer 2023.
© Photo by Lucky Ai on Adobe Stock






